There are several situations in which expected (present values of) payouts
can be computed using an evolution equation that has time moving backwards
from the future to the present. The basic idea comes through clearly in the
simple case of an undiscounted terminal payout. At the terminal time, T,
we get a payout that depends on the state of the system at that time:
![]() . We want to compute the expected value of this payout:
. We want to compute the expected value of this payout:
![]()
To compute this, we compute a connected collection of expectation values, f(x,t), defined as
We find a relationship between these numbers by considering one step of
the Markov chain. If the system is in state x at time t, then the
probability for it to be at state y at the next time is
![]() .
For expectation values, this implies
.
For expectation values, this implies
This relation is used to compute (5) as follows. The final time values,
f(x,T) are the given values ![]() . From these, we compute all the
numbers f(x,T-1) using (7) with t=T-1. Continuing like this, we
eventually get to t=0. We may know X(0), the state of the system
at the current time. Otherwise we can use
. From these, we compute all the
numbers f(x,T-1) using (7) with t=T-1. Continuing like this, we
eventually get to t=0. We may know X(0), the state of the system
at the current time. Otherwise we can use
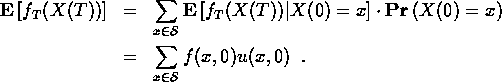
All the values on the bottom line should be known.
As with the probability evolution equation ( ), the
equation for the evolution of the expectation values (
), the
equation for the evolution of the expectation values ( )
can be written in matrix form. The difference from the probability evolution
equation is that here we arrange the numbers
)
can be written in matrix form. The difference from the probability evolution
equation is that here we arrange the numbers ![]() into a
column vector,
into a
column vector, ![]() . The evolution equation for the
expectation values is then written in matrix form as
. The evolution equation for the
expectation values is then written in matrix form as
This time, the vector goes on the right. If apply ( )
repeatedly, we get, in place of (
)
repeatedly, we get, in place of ( ),
),
There are several useful variations on this theme. For example, suppose that we have a running payout rather than a final time payout. Call this payout g(x,t). If X(t) = x then g(x,t) is added to the total payout that accumulates over time from t=0 to t=T. We want to compute
![]()
As before, we find this by computing more specific expected values:
![]()
These numbers are related through a generalization of (7) that takes into account the known contribution to the sum from the state at time t:
![]()
The ``initial condition'', given at the final time, is
![]()
This includes the previous case, we take ![]() and
g(x,t) = 0 for t ;SPMlt; T.
and
g(x,t) = 0 for t ;SPMlt; T.
As a final example, consider a path dependent discounting. Suppose for a
state x at time t there is a discount factor r(x,t) in the range
![]() . A cash flow worth f at time t+1 will be
worth r(x,t)f at time t if X(t) = x. We want the discounted value
at time t=0 at state X(0) = x of a final time payout worth
. A cash flow worth f at time t+1 will be
worth r(x,t)f at time t if X(t) = x. We want the discounted value
at time t=0 at state X(0) = x of a final time payout worth
![]() at time T. Define f(x,t) to be the value at time t
of this payout, given that X(t) = x. If X(t) = x then the time
t+1 expected discounted (to time t+1) value is
at time T. Define f(x,t) to be the value at time t
of this payout, given that X(t) = x. If X(t) = x then the time
t+1 expected discounted (to time t+1) value is
![]()
This must be discounted to get the time t value, the result being
![]()