 ) and the backward
equation (
) and the backward
equation ( ) are connected
through a duality relation. For any time t, we compute (
) are connected
through a duality relation. For any time t, we compute ( ) as
) as
The forward evolution equation ( ) and the backward
equation (
) and the backward
equation ( ) are connected
through a duality relation. For any time t, we compute (
) are connected
through a duality relation. For any time t, we compute ( ) as
) as
For now, the main point is that the sum on the bottom line does not depend on t. Given the constancy of this sum and the u evolution equation (4), we can give another derivation of the f evolution equation (7). Start with
![]()
Then use (4) on the left side and rearrange the sum:
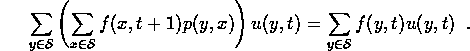
Now, if this is going to be true for any u(y,t), the coefficients of u(y,t) on the left and right sides must be equal for each y. This gives (7). Similarly, it is possible to derive (4) from (7) and the constancy of the expected value.
The evolution equations (4) and (7) have some qualitative properties in
common. The main one being that they preserve positivity. If
![]() for all
for all ![]() , then
, then ![]() for
all
for
all ![]() also. Likewise, if
also. Likewise, if ![]() for all x,
then
for all x,
then ![]() for all x. These properties are simple consequences
of (4) and (7) and the positivity of the p(x,y). Positivity preservation
does not work in reverse. It is possible, for example, that
f(x,t+1) ;SPMlt; 0 for some x even though
for all x. These properties are simple consequences
of (4) and (7) and the positivity of the p(x,y). Positivity preservation
does not work in reverse. It is possible, for example, that
f(x,t+1) ;SPMlt; 0 for some x even though ![]() for all x.
for all x.
The probability evolution equation (4) has a conservation law not shared by (7). It is
![]()
independent of t. This is natural if u is a probability distribution, so that the constant is 1. The expected value evolution equation (7) has a maximum principle
![]()
This is a natural consequence of the interpretation of f as an expectation value. The probabilities, u(x,t) need not satisfy a maximum principle either forward of backward in time.
This duality relation has is particularly transparent in matrix terms.
The formula ( ) is expressed explicitly in terms of the
probabilities at time t as
) is expressed explicitly in terms of the
probabilities at time t as
![]()
which has the matrix form
![]()
Written in this order, the matrix multiplication is compatible; the other
order, ![]() , would represent an
, would represent an ![]() matrix instead of a single number. In view of (
matrix instead of a single number. In view of ( ), we may
rewrite this as
), we may
rewrite this as
![]()
Because matrix multiplication is associative, this may be rewritten
![]()
for any t. This is the same as saying that
![]() is independent of t, as we already saw.
is independent of t, as we already saw.
In linear algebra and functional analysis, ``adjoint'' or ``dual''
is a fancy generalization of the transpose operation of matrices. People
who don't like to think of putting the vector to the left of the matrix
think of ![]() as multiplication of (the transpose of)
as multiplication of (the transpose of)
![]() , on the right, by the transpose (or adjoint or dual) of
P. In other words, we can do enough evolution to compute an expected
value either using P its dual (or adjoint or transpose). This is the
origin of the term ``duality'' in this context.
, on the right, by the transpose (or adjoint or dual) of
P. In other words, we can do enough evolution to compute an expected
value either using P its dual (or adjoint or transpose). This is the
origin of the term ``duality'' in this context.