| Back to . . . | This section . . . |
|
|
QuickTime movie showing how a two-bladed Archimedes screw lifts water.
Large: 416 x 320 pixels, 183 kilobytesSet your movie player to "Loop" so that the screw will continuously turn. Make sure your movie player shows all 21 frames; otherwise you will see undesirable stroboscopic effects. |
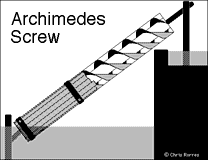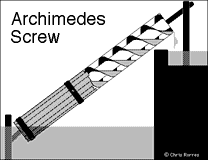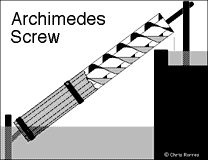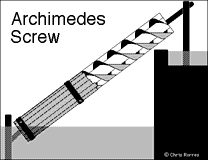
 Two-bladed screw
Two-bladed screw
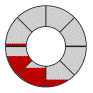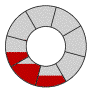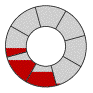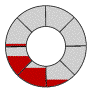 Eight-bladed screw
Eight-bladed screw
|
Here are two QuickTime movies showing the cross-sections of a two-bladed and eight-bladed Archimedes screw as they revolve. You can download the following sizes of these movies (all are 34 frames long at 30 frames/second):
Two-bladed:Set your movie player to "Loop" so that the screw will continuously turn. Make sure your movie player shows all 34 frames; otherwise you will see undesirable stroboscopic effects. The two-bladed cross-section is for the screw whose profile is in the first figure. The eight-bladed screw has the same profile, but with four times as many blades. An example of a two-bladed screw is shown in the two illustrations of modern Egyptian farmers. |
The rotation of the screw is clockwise when looking down from the top water level. Each turn of the screw empties two "buckets" of water of the two-bladed screw and eight buckets of the eight-bladed screw. The angle of inclination of the screw is that determined by a 3-4-5 triangle (what Virtruvius calls a "Pythagorean right-angled triangle"), which is 36.870° (a slope of 3/4).
Mathematical notes: The slope of the outside of the screw's helical blades with respect to its sides is 2. This requires that the slope the screw makes with respect to a horizontal line be less that 2 (an angle of 63.435°) in order for the buckets or pockets of water to form. In the profile of the screw the projection of each helical blade consists of two sinusoidal curves with the same periods and phases. One has an amplitude equal to the radius of the outer cylinder and the other has an amplitude equal to the radius of the inner cylinder. The horizontal water level of each full bucket of water is tangent to the inner sinusoidal curve. Thus, if the equation on the inner sinusoidal curve is y = sin x, then the water level is tangent to it at x = arccos(-3/4) = 138.59°.