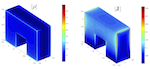
QBX: A Quadrature Method for Layer Potentials in Complex Geometries
Integral equation methods for the solution of partial differential equations,
when coupled with suitable fast algorithms, yield geometrically flexible,
asymptotically optimal and well-conditioned schemes in either interior
or exterior domains. In order to high-order accuracy, however,
one must accurately evaluate boundary integrals with singular,
weakly singular or nearly singular kernels. Historically, these issues
have been handled either by low-order product integration rules (computed
semi-analytically), by singularity subtraction/cancellation, by kernel
regularization and asymptotic analysis, or by the construction of special
purpose “generalized Gaussian quadrature” rules.
We have recently created a new systematic,
general-purpose, and high-order scheme that can be used for
any singularity (including hypersingular kernels).
The method is based only on the
assumption that the field induced by the integral operator is locally
smooth when restricted to either the interior or the exterior.
Discontinuities in the field across the boundary are permitted. The scheme,
denoted QBX (quadrature by expansion), is easy to implement and compatible
with fast hierarchical algorithms including the fast multipole method.
-
A. Kloeckner, A. Barnett, L. Greengard, and M. O'Neil,
Quadrature by Expansion: A new method for the evaluation of
layer~potentials,
J. Comput. Phys., 252, 332-349 (2013).
-
C. Epstein, L Greengard, and A. Kloeckner,
On the convergence of local expansion of
layer~potentials,
SIAM J. Numer. Anal., {\bf 51}, 2660--2679 (2013).
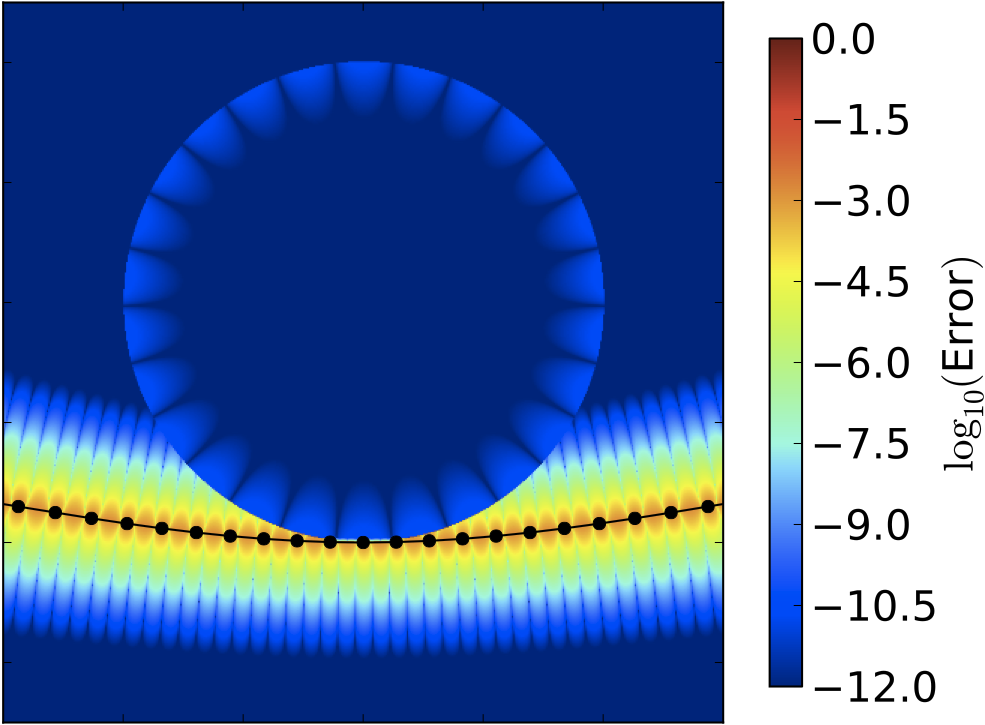Placing an expansion center near, but off the boundary, we have
shown that high order accuracy can be achieved through the use of a
local expansion of the induced field, which is "one-sided" smooth.
The error in the field evaluation is plotted (from [1]).
