Multimaterial Interfaces
The interaction of acoustic or electromagnetic waves with structured
materials is often complicated by the fact that the scattering
geometry involves domains where multiple media meet at a single point.
Examples include the design of
diffraction gratings, the development of high efficiency solar cells,
and non-destructive optical inspection in semiconductor manufacturing
(metrology). We have developed integral equation methods for the
calculation of two-dimensional scattering from both compact and
periodic structures.
Our approach involves the modification of a standard integral
representation, the use of adaptive refinement at geometric
singularities, and (most recently) the development of a fast direct solver,
which permits the rapid calculation of scattering from a fixed structures
at multiple angles of incidence.
L. Greengard and J.-Y. Lee,
Stable and accurate integral equation methods for scattering
problems with multiple material interfaces in two dimensions ,
J. Comput. Phys., 231 , 2389-2395 (2012).
L. Greengard, K. L. Ho, and J.-Y. Lee,
A fast direct solver for scattering from periodic structures
with multiple material interfaces in two dimensions ,
J. Comput. Phys., 258 , 738-751 (2014).
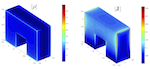
The figure shows two copies of an infinite array of scatterers arrange
on the surface of a dielectric substrate. The upper half-space, the lower
half-space and the trapezoidal-shaped domains all have different
dielectric constants. The electromagnetic field is
singular where they meet ("triple points"), causing convergence problems
for standard numerical methods.
