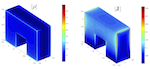
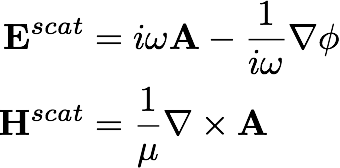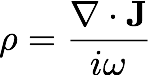Integral Equation Theory
A major initiative in our group concerns the development of
integral equation methods that are well-conditioned and not
subject to spurious resonances or low-frequency breakdown.
The classical formulation of
the Maxwell equations uses the vector and scalar potential with current
as a surface unknown:
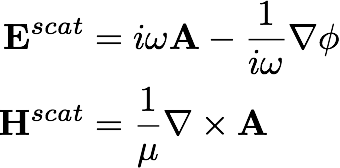
One of the fundamental difficulties with this approach is that as the
frequency ω
goes to zero, the representation for
E blows up
(as is evident from the formula above).
At non-zero frequency, this leads to what is called
low-frequency breakdown - that is,
catastrophic ill-conditioning as a surface discretization is refined in
a sub-wavelength regime to account for complicated geometric features.
Standard formulations can also suffer from ill-conditioning and lack
of invertiblity for certin values of ω.
Generalized Debye formulations
We have recently developed a representation based on two scalar unknowns that
leads to integral equations which are well-conditioned, do not suffer from
low frequency breakdown, and are free of spurious resonances.
C. Epstein and L. Greengard,
Debye sources and the numerical solution
of the time harmonic Maxwell equations,
Comm. Pure Appl. Math., 63 , 413-463, (2009).
C. Epstein, L. Greengard, and M. O'Neil,
Debye sources and the numerical solution
of the time harmonic Maxwell equations II,
Comm. Pure Appl. Math., 66 , 753-789, (2013).
Charge current formulations
A complementary approach to avoiding low frequency breakdown
involves the use of charge as an auxilliary variable
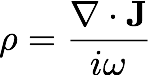
instead of using the current
J alone.
We have recently shown that
by solving a second (scalar) integral
equation for the charge, one can
overcome a loss of precision in computing the electric field after
solving the magnetic field integral equation.
F. Vico, Z. Gimbutas, L. Greengard and M. Ferrando-Bataller,
Overcoming Low-Frequency Breakdown of the Magnetic Field
Integral Equation ,
IEEE Trans. Antennas and Propagation, 61 , 1285-1290 (2013).
For multiply connected domains,
we have recently shown that,
at zero frequency, the standard boundary
conditions on the tangential components of the magnetic field do not
uniquely determine the vector potential but that a
(gauge-invariant) consistency condition overcomes this
non-uniqueness. This resolves a longstanding difficulty in inverting
the magnetic field integral equation.
C. L. Epstein, Z. Gimbutas, L. Greengard, A. Kloeckner, and
M. O'Neil,
A Consistency Condition for the Vector Potential in
Multiply-Connected Domains ,
IEEE Trans. Magnetics, 49 1072-1076 (2013).
We are currently developing a systematic framework for
studying the condition number of integral equation methods for
electromagnetic and acoustic scattering, by
obtaining expressions for the signatures of layer potentials
in the spherical harmonic or vector spherical harmonic basis.
This permits, among other things, a study of the selection of
certain parameters in "combined field" and
"Calderon-preconditioned" formulations,
extending earlier work by Kress and others.
Felipe Vico, Leslie Greengard, and Zydrunas Gimbutas,
Boundary integral equation analysis on the sphere,
submitted.