Fast Direct Solvers
One drawback to FMM-accelerated solvers is that they rely on an
underlying iterative strategy. Each change to the structure
and each new electromagnetic excitation requires a restart of the
solution process. In design, however, one needs to solve an enormous
number of
forward problems
as part of an optimization loop, and the geometry or material properties
are often modified in a local fashion.
In the last few years, a number of groups have
begun the development of a new class of fast algorithms
that is aimed at significantly enhance our ability to deal with such problems.
The basic goal is to create fast direct solvers which first compute a
new type of factorization using
O(N^α) operations with
1 < α < 2 , followed by a step
requiring
O(N log N) operations for each
subsequent right-hand side and/or low-rank perturbation of the
system matrix.
The essence of the technical approach is simple,
although the work is quite involved;
instead of using fast multipole-type analysis to ``compress" the far-field
representation of a piece of scatterer, we derive
compressed representations of pieces of the inverse matrix.
These are then combined systematically to yield the full inverse
operator. More importantly, these pieces can be reused in a design loop.
Our numerical experiments have shown that the
inverse
of a dense
40,000 x 40,000 matrix corresponding to an
electrostatic boundary value problem can be applied in
0.1
seconds on a standard workstation (after a somewhat expensive
precomputation phase requiring about 15 minutes).
For comparison, a single FMM iteration for this
number of degrees of freedom would take 2-3 seconds and inversion would
require about 20 such iterations.
Carrying this procedure out for the full Maxwell system at high frequencies
is an active area of research.
-
L. Greengard, D. Gueyffier, P.-G. Martinnson and V. Rokhlin,
Fast Direct Solvers for Integral Equations in Complex
Three-Dimensional Domains,
Acta Numerica, 243-275 (2009).
-
K. L. Ho and L. Greengard,
A Fast Direct Solver for Structured Linear Systems
by Recursive Skeletonization,
SIAM J. Sci. Comput., 35 A2507-A2532 (2012).
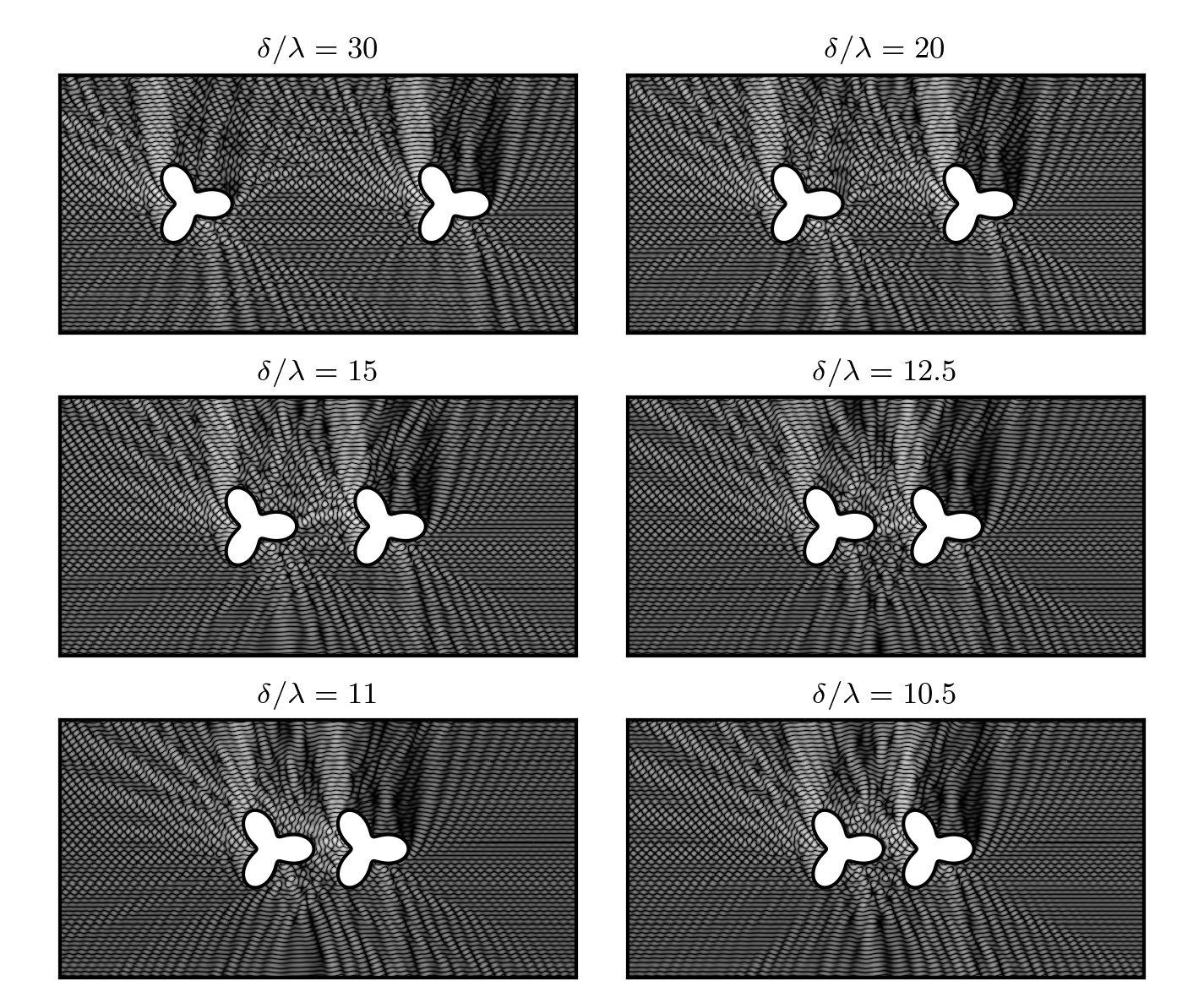This figure shows the intensity of the acoustic pressure field in
response to an incoming plane wave for a succession of scattering
geometries. The fast direct
solver was used to compute the response of each scatterer alone.
The compressed inverse was then used as a preconditioner for each new
geometry, reducing the number of iterations required from 700 to 10
(from [2]).
