S O U R C E S
| Back to . . . |
This section . . .
|
|
Diodorus Siculus (c. first century BC), Bibliotheke, Book I, 34.2
For since it [the delta of the Nile River] is alluvial soil and well watered, it produces many crops of every kind, inasmuch as the river by its annual rise regularly deposits on it fresh slime, and the inhabitants easily irrigate its whole area by means of a contrivance which was invented by Archimedes of Syracuse and is called, after its shape, a screw.(Translation by C. H. Oldfather in Diodorus Siculus, Library of History, Volume I, Loeb Classical Library, Harvard University Press, Cambridge, 1933.)
Diodorus Siculus (c. first century BC), Bibliotheke, Book V, 37.3-4
. . . and what is the most surprising thing of all, they [Roman slaves] draw out the water of the streams they encounter [in Spanish mines] by means of what is called by men the Egyptian screw, which was invented by Archimedes of Syracuse at the time of his visit to Egypt; and by the use of such screws they carry the water in successive lifts as far as the entrance, drying up in this way the spot where they are digging and making it well suited to the furtherance of their operations. Since this machine is an exceptionally ingenious device, an enormous amount of water is thrown out, to one's astonishment, by means of a trifling amount of labour, and all the water from such rivers is brought up easily and from the depths and poured out on the surface. And a man may well marvel at the inventiveness of the craftsman [Archimedes], in connection not only with this invention but with many other greater ones as well, the fame of which has encompassed the entire inhabited world . . .
(Translation by C. H. Oldfather in Diodorus Siculus, Library of History, Volume III, Loeb Classical Library, Harvard University Press, Cambridge, 1939.
Diagram from R. E. Palmer, “Notes on Some Ancient Mine Equipments and Systems,” Transactions of the Institution of Mining and Metallurgy, Volume 36, Pages 299-336, 1926.)
Athenaeus of Naucratis (c. AD 200), Deipnosophistae, Book V
The bilge-water [of the ship Syracusia], even when it became very deep, could easily be pumped out by one man with the aid of the screw, an invention of Archimedes.(Translation by Charles Burton Gulick in Athenaeus, Deipnosophists, Loeb Classical Library, Harvard University Press, Cambridge, 1928)
Leonhard Euler (1707-1783), The Fourteen “Quaestiones Mathematicae”
1. A theory is sought for the rising of water by the screw of Archimedes. Even if this machine is used most frequently, still its theory is desired.(The first of fourteen mathematical problems that this great Swiss mathematician read before the St. Petersburg Academy of Science (St. Petersburg, Russia) in 1757 to be considered as potential problems for the Academy's prize.)
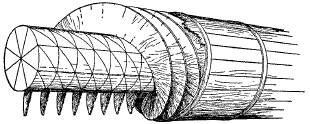
Vitruvius (c. first century BC), De Architectura, Book X, Chapter VI, The Water Screw
1. There is also the method of the screw, which raises a great quantity of water, but does not carry it as high as does the wheel. The method of constructing it is as follows. A beam is selected, the thickness of which in digits is equivalent to its length in feet [16 digits = 1 foot]. This is made perfectly round. The ends are to be divided off on their circumference with the compass into eight parts, by quadrants and octants, and let the lines be so placed that, if the beam is laid in a horizontal position, the lines on the two ends may perfectly correspond with each other, and intervals of the size of one eighth part of the circumference of the beam may be laid off on the length of it. Then, placing the beam in a horizontal position, let perfectly straight lines be drawn from one end to the other. So the intervals will be equal in the directions both of the periphery and of the length. Where the lines are drawn along the length, the cutting circles will make intersections, and definite points at the intersections.
CONSTRUCTION OF THE WATER SCREW
2. When these lines have been correctly drawn, a slender withe of willow, or a straight piece cut from the agnus castus tree, is taken, smeared with liquid pitch, and fastened at the first point of intersection. Then it is carried across obliquely to the succeeding intersections of longitudinal lines and circles, and as it advances, passing each of the points in due order and winding round, it is fastened at each intersection; and so, withdrawing from the first to the eighth point, it reaches and is fastened to the line to which its first part was fastened. Thus it makes as much progress in its longitudinal advance to the eighth point as in its oblique advance over eight points. In the same manner, withes for the eight divisions of the diameter, fastened obliquely at the intersections on the entire longitudinal and peripheral surface, make spiral channels which naturally look just like those of a snail shell.3. Other withes are fastened on the line of the first, and on these still others, all smeared with liquid pitch, and built up until the total diameter is equal to one eighth of the length. These are covered and surrounded with boards, fastened on to protect the spiral. Then these boards are soaked with pitch, and bound together with strips of iron, so that they may not be separated by the pressure of the water. The ends of the shaft are covered with iron. To the right and left of the screw are beams, with crosspieces fastening them together at both ends. In these crosspieces are holes sheathed with iron, and into them pivots are introduced, and thus the screw is turned by the treading of men.
4. It is to be set up at the inclination corresponding to that which is produced in drawing the Pythagorean right-angled triangle: that is, let its length be divided into five parts; let three of them denote the height of the head of the screw; thus the distance from the base of the perpendicular to the nozzle of the screw at the bottom will be equal to four of those parts. A figure showing how this ought to be has been drawn at the end of the book, right on the back.
I have now described as clearly as I could, to make them better known, the principles on which wooden engines for raising water are constructed, and how they get their motion so that they may be of unlimited usefulness through their revolutions.
(Translation and diagram by Morris Hicky Morgan in Vitruvius: The Ten Books on Architecture, Harvard University Press, Cambridge, 1914, pages 295-297.
The following Latin text is available online: Vitruvius’s De Architetura libri decem published by Daniele Barbaro in Venice in 1567. See page 346.)