On Floating Bodies (Book II)

Back to . . .

This page . . .

Below is the abstract of a recent article written by the Webmaster of this site (Chris Rorres) that appeared in The Mathematical Intelligencer published by Springer Publishing House. You can download a reprint of the complete article from the following link:

R E P R I N T [PDF version (664 kilobytes)]

Following the abstract are links to QuickTime movies that illustrate the figures in the paper, and also to high-resolution jpegs of those figures.

Two overviews of this article can be found in Ivars Peterson’s online columns in Science News Online (MATHTREK: 21 August 2004) and Science News for Kids (MUSE: January 2005).

Two more overviews, by science writer Dana Mackenzie, can be found in Science magazine (“Whatever floats your paraboloid”, Volume 305, Number 5687, 20 August 2004, page 1102) and in Discover magazine (“Tilt”, Volume 26, Number 07, July 2005, pages 36-37).

Another overview as it applies to the stability of kayaks was printed in Mountain Gazette magazine (“The occupation of floating bodies” by B. Frank, Number 123, April 2006).

[Remark: The animated figure in the upper-lefthand corner illustrates the seven equilibrium positions (both stable and unstable) of a floating paraboloid whose height is 0.88 times its diameter and whose relative density is 0.51. The seven tilt angles are 0°(base up), 32.4°, 61.4°, 95.8°, 118.7°, 140.8°, and 180°(base down).]

A BSTRACT

The Mathematical Intelligencer
Volume 26, Number 3, Summer 2004, pp. 32-42

COMPLETING BOOK II OF ARCHIMEDES’S
ON FLOATING BODIES

By Chris Rorres

Archimedes (c. 287 BC to 212/211 BC) lived in the Greek city-state of Syracuse, Sicily, up to the time that it was conquered by the Romans, a conquest that led to his death. Of his works that survive, the second of his two books of On Floating Bodies is considered his most mature work, commonly described as a tour de force. This book contains a detailed investigation of the stable equilibrium positions of floating right paraboloids of various shapes and relative densities, but restricted to the case when the base of the paraboloid lies either entirely above or entirely below the fluid surface.
This paper summarizes the results of research in which I completed Archimedes’s investigation to include also the more complex cases when the base of the floating paraboloid is partially submerged. Modern scientific computing and computer graphics enabled me to construct a three-dimensional surface that summarizes all possible equilibrium positions (both stable and unstable) for all possible shapes and relative densities. This equilibrium surface contains folds and cusps that explain certain catastrophic phenomena— for example, the sudden tumbling of a melting iceberg or the toppling of a tall structure due to liquefaction of the ground beneath it— that have long been observed but not previously explained fully.

QUICKTIME MOVIES

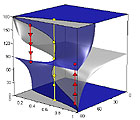
Equilibrium Surface (animations of Fig. 5 in paper)
In the following four movies the equilibrium tilt angles θ in [0°, 180°] are plotted for values of the base angle φ in [0°, 90°] and values of the relative density s in [0, 1]. The resulting equilibrium surface is shown in oblique view and rotates 360°. The movies are 450 x 450 pixels, 4-6 MB, 6 seconds, 180 frames, and 30 frames/second.

QuickTime Movie : AS points in blue and US points in gray as shown in Fig. 5 of paper.
QuickTime Movie : AS points in blue and US points in gray. No tick marks or other markings.
QuickTime Movie : Points with base not cut by fluid surface in black. Points with base cut by fluid surface in gold. Curve of points with base cut by fluid surface at exactly one point in red. Curve of NS points in black.
QuickTime Movie : Stereoview of the rotating equilibrium surface as in Fig. 5. (400 x 200 pixels, 3 MB)

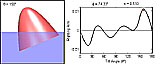
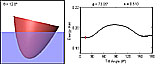
Righting-Arm Curve and Energy-Arm Curve (animations of Fig. 3 in paper)
In these four movies the righting arm or the energy arm is plotted for all values of the tilt angle θ. The paraboloid, which has base angle φ = 74.330° and relative density s = 0.510, is shown in a profile or an oblique view. All movies are 600 x 240 pixels, 4.5 MB, 12 seconds, 180 frames, and 15 frames/second.

QuickTime Movie : Righting Arm vs. Tilt Angle (profile view of paraboloid)
QuickTime Movie : Righting Arm vs. Tilt Angle (oblique view of paraboloid)
QuickTime Movie : Energy Arm vs. Tilt Angle (profile view of paraboloid)
QuickTime Movie : Energy Arm vs. Tilt Angle (oblique view of paraboloid)

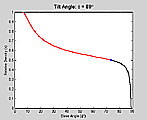
Tilt Angle Slices (animations of Fig. 7A-D in paper)

QuickTime Movie
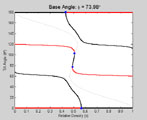
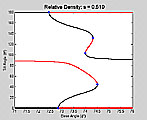
In this movie the tilt angle θ varies from 0° to 180° in one-degree steps. The AS points are in black, the US points are in red, and the NS points are in blue.
(550 x 450 pixels, 928 kb, 12 seconds, 181 frames, 15 frames/second)

Base Angle Slices (animations of Fig. 7E-H in paper)
In these movies the base angle φ varies over the indicated values. The AS points are in black, the US points are in red, and the NS points are in blue. The light gray curve in the background is the projection of the curve of NS points onto the slice. All are 550 x 450 pixels and 15 frames/second.

QuickTime Movie : φ varies from 0° to 90° in increments of 1°. (436 kb, 6 seconds, 91 frames)
QuickTime Movie : φ varies from 60° to 90° in increments of 0.1°. (1.5 MB, 20 seconds, 301 frames)
QuickTime Movie : φ varies from 73° to 75° in increments of 0.01°. (977 kb, 13 seconds, 201 frames)
QuickTime Movie : φ varies from 74.15° to 74.25° in increments of 0.001°. (405 kb, 6 seconds, 101 frames)

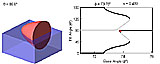
Relative Density Slices (animations of Fig. 7I-L in paper)
In these movies the relative density s varies over the indicated values. The AS points are in black, the US points are in red, and the NS points are in blue. All are 550 x 450 pixels, 6 seconds, 101 frames, 15 frames/second.

QuickTime Movie : s varies from 0 to 1 in increments of 0.01. Base angle: 0° ≤ φ ≤ 90°. (545 kb)
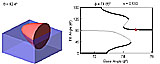
QuickTime Movie : s varies from 0 to 1 in increments of 0.01. Base angle: 60° ≤ φ ≤ 90°. (570 kb)
QuickTime Movie : s varies from 0.45 to 0.55 in increments of 0.001. Base angle: 71° ≤ φ ≤ 76°. (652 kb)

Hysteresis Loop (animations of Fig. 7J of the paper)
In these movies the relative density s of a paraboloid is kept fixed at 0.499 and its base angle φ oscillates between 73.76°. and 74.42°, changing by increments of ±0.02°. Both movies are 600 x 240 pixels, 1.5 MB, 4 seconds, 66 frames, and 15 frames/second.

QuickTime Movie
An oblique view of the paraboloid is shown together with a slice of the equilibrium surface.

QuickTime Movie
A profile view of the paraboloid is shown together with a plot of the energy arm vs. the tilt angle.

Turning a Paraboloid Upside-Down (animations of Fig. 7L of paper)
In these movies the relative density s of a paraboloid is kept fixed at 0.510 and its base angle φ goes from 72° to 75° and then back to 72°. The tilt angle θ starts at 0° and ends up at 180° after undergoing two jumps at 42.4° (to 93.4°) and 98.8° (to 145.3°). All are 600 x 240 pixels, 2.8 MB, 8 seconds, 121 frames, and15 frames/second.

QuickTime Movie
An oblique view of the paraboloid is shown together with a slice of the equilibrium surface.

QuickTime Movie
An oblique view of the paraboloid is shown together with a plot of the energy arm vs. the tilt angle.

QuickTime Movie
A profile view of the paraboloid is shown together with a plot of the energy arm vs. the tilt angle.

Tumbling Iceberg (animations of Fig. 8 of the paper)

QuickTime Movie
The base angle φ of a paraboloid with relative density s of 0.9 increases from 82° to 83° in increments of 0.01°. The iceberg is initially floating vertically at a tilt angle θ of 0° and then tumbles over when its base angle passes through 82.65°. A profile view of the iceberg is shown together with a plot of the energy arm vs. the tilt angle.
(600 x 240 pixels, 2.2 MB, 6.3 seconds, 101 frames,15 frames/second)

QuickTime Movie
The same as above, except an oblique view of the iceberg is shown.
(600 x 240 pixels, 2.3 MB, 6.3 seconds, 101 frames,15 frames/second)

Toppling Structure due to Soil Liquefaction (animation of Fig. 9 of the paper)

QuickTime Movie
The relative density s of a paraboloid of base angle 80° increases from 0 to 0.2 and then decreases back to 0 in increments of 0.01 and 0.0001. The paraboloid is initially standing vertically at a tilt angle θ of 180° and then topples over when its relative density passes through 0.187. A profile view of the paraboloid is shown together with a plot of the energy arm vs. the tilt angle.
(600 x 240 pixels, 1.3 MB, 3.3 seconds, 59 frames, 15 frames/second)

F IGURES

Click on a thumbview below to view or download a high-resolution JPEG file of any of the nine figures in the paper.

These figures are copyrighted by Springer Publishing House and should not be reproduced elsewhere without permission.

Fig. 1: 2285 x 697 pixels, 151 kilobytes

Fig. 4: 2673 x 1196 pixels, 389 kilobytes

Fig. 7: 2400 x 1800 pixels, 446 kilobytes
Fig. 2: 913 x 302 pixels, 23 kilobytes

Fig. 5: 1407 x 1876 pixels, 318 kilobytes

Fig. 8: 2188 x 625 pixels, 112 kilobytes
Fig. 3: 2321 x 1625 pixels, 347 kilobytes

Fig. 6: 2350 x 1250 pixels, 200 kilobytes

Fig. 9: 2188 x 1250 pixels, 134 kilobytes

Photograph of Author (Chris Rorres)

The author is shown with two Archimedes-inspired finials he designed for his fence at home. The top one is a sphere atop a cylinder illustrating the so-called “tombstone” theorem that Archimedes considered his most important, that the volume and surface area of a sphere are both two-thirds, respectively, of the volume and surface area of its circumscribing cylinder. The bottom finial illustrates a theorem that Archimedes used for his research in floating paraboloids; namely, that the volume of a right paraboloid is one-half the volume of its circumscribing cylinder.

jpeg file : 1300 x 960 pixels, 302 kilobytes *